Bach/Trapani Fugues and Canons Notes

Notes about Notes

J. S. Bach, Prelude and Fugue in B minor || Christopher Trapani Canon A (Four Bells) and Canon B (Convex Mirror)

I. Patterns

Into the snowballing mass of unknowns that constitutes our collective present, I’d like to place one more question — an old question, a simple question — which might possibly provide solace or perspective: What do notes do? How do these flocks of dots – indicating frequencies, ratios, and the passage of time – behave? How do they persist in culture and memory, written or unwritten? They walk; they speak; they sit in libraries; they fill bars; they fly through the air; all without ever having been seen. They anticipate that lines and curves be drawn between them, and use those lines to point toward the future – or at least its next few seconds - with extraordinary clarity. Even the unplayed notes, sitting silent, awaiting possible employment, and become awfully active if given the chance. Strange things, these notes, these dots that would be waves, lying in wait.

Johann Sebastian Bach seems to have captured something essential about the geometry of notes. In his vast and encyclopedic body of work, he managed to engage and exploit something fundamental in their potential for order, meaning, representation, and expression. On the one hand, it is true that he wrote works within the everyday realities of church, doctrine, personnel, employment, teaching and the demands of the earthly calendar. But then, within his notes, there is a wild excess of independent systems which form a weirdly huge sonic-numerical jungle. His works and sets of works seem often to be set up in powers of two and three: Six Sonatas and Partitas for violin (alternating type); twenty-four preludes and fugues (in twelve keys) in the Well-tempered Clavier; thirty-two 'Goldberg' Variations, defined in groups of three by canons at steadily rising intervals, to name just a few famous examples. Once set in motion, the patterns seem almost to generate themselves. And if there were any doubt as to just how 'angels-on-the-head-of-a-pin' esoteric this numerological jungle can become, one need look no further than the musicological argument as to whether the spirals at the top of the manuscript of the Well-Tempered Clavier represent a system of tuning (which is itself a struggle between powers-of-three and powers-of-two) that would affect every well-chosen note of every well-tempered piece:

It is perhaps enough to say that in the works of J.S.Bach the level of abstraction and mystery within the notes alone is extraordinarily high. And, there really does seem to be some intention in it all – even in the casual, droodle-y little decoration shown above. Any swirl of the pen seems able to yield something which might alter the meaning not only of the of twenty-four keyboard pieces, but even of the instrument itself.

The last fugue of the Well-Tempered Clavier implies the depth and layering of this pattern-consciousness. Set in the precarious key of b minor (having almost spiraled back to the C Major of the first work in the set), Bach builds a final fugue theme on all twelve notes, as if to sum up all the twelve key signatures of all the previous pieces. Here, again, there are spirals in the spirals, repetitions in the repetitions, cycles in the cycles, showing deep patterns in the smallest details.

The preceding Prelude seems simply to explore the relationship between scales in a walking bass and ascending intervals. Its music moves elegantly, providing something not distant from the sensation of simply being awake. The depth and ceremony of the fugue stands out in severe contrast, and so they form something of a pair, in counterpoint.

II. Canons

Briefly put: a canon takes a compact, identifiable musical idea and repeats it after some interval, applying transformations (up/down, forward/backward, upside-down, compressed, stretched, distorted) in ways that can make curious sense. Bach famously wrote a lot of extraordinarily clever canons. They serve as a fairly natural tool for studying musical development, since they engage and develop a sharply definable relationship between musical pattern and human memory.

But Bach's techniques, rich as they are, are not the only ones. Christopher Trapani writes:

I tried to rethink what a canon might mean and how some previously unfamiliar kind of interaction between two voices could be achieved — not an easy thing, given that we are very accustomed to hearing canons in a specific way.

Taking this a bit further: canons may also be considered as naturally occurring, and not merely as snowmen of music theory. They work because they echo the fact of echoing, because they mirror the fact of mirroring, and because they test the power (and malleability) of repetition in memory. It is not only true that we recognize repetitions; it is also true (or equally true) that phenomena may create repetitive patterns. In this way, canons might simply... arise.

Trapani’s Canon A (Four Bells) and Canon B (Convex Mirror) bring us two examples of phenomenally defined canons, written for piano. (These two pieces are part of a commission by the Charlottesville Chamber Music Festival and Benjamin Hochman, and will be part of a larger set.) Canon A is based on a transcription of bell sounds from Palermo, Italy, a recording of which the composer has been kind enough to provide here, as an 'ur-context' for the first canon:

After the transcription, he maintains not only the note-patterns of the bells, but also their fundamental instability:

Rather than creating a mathematically perfect polyrhythm, I wanted to transcribe the imperfections of the bells tolling against a constant tempo.

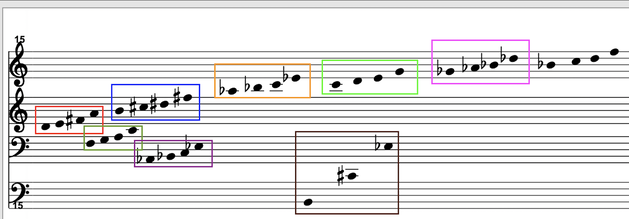The bell sounds (red box) reappear in different registers, mostly higher.

Several levels of transformation follow, as the lightly unpredictable repetition of each bell seems to take on a possible role in a larger musical identity. And perhaps the most important transformation, on a different scale, is that the bell-tones must be literally grasped by the pianist; the performer must know them not only as bells but as potential musical content; in this way the music takes on not only the sound content of the bells but also an element of human contact. The humanization — or at least reduction to ‘notes’ — of the bell sequence then allows some of the traditional canon transformations to appear. Most notable is the repetition at higher pitch (see also: Bach’s ‘Endlessly Rising Canon’ from the Musical Offering). But the bells themselves remain present, transcribed, keeping their own music even in the piano, and eventually disappearing, as bells do when their swing is no longer sufficient, and contact fails.

Initially the mirroring is clear to see, creating a 'butterfly' shape between the upper (stem-up) and lower (stem-down) voices

Canon B (Convex mirror) brings other traditional techniques of canon-writing as a jumping-off point. Especially the technique of inversion allows that a musical motive be repeated upside-down in such a way as to preserve an audible relationship. But in this case, the mirror is distorted, and becomes more evidently so as the canon progresses.

The bottom voice is a reflection of the top voice, but you have to imagine that after identifying the midpoint of each phrase... the second voice is rhythmically altered to either spread to the edges or slightly tighten to the midpoint of the phrase. Hence the convex mirror concept.

Even the lens-shaped motives cannot be understood as the cause or effect of the transformation -- are they the mirror or the reflection? Eventually they take on more and more distended time-scales and shapes. Their undulations remain palpable, but their synchrony and pitches wander. Their solution, or dissolution, is left to your ear.

So what are these relationships between notes, between groups of notes, between forms, between voices? We only know that they can be played, and played with. They are music when they cohere, they are music as they wander; they are music where they stand, and they are music while they fade. They seek each other, they seek themselves; they pass in time, they tell us the time; they make us count, they make us lose count. And for some reason, we keep following, almost as though they might lead somewhere.